Why it is so wrong to average ratios: Simpson's paradox

-

As a statistics major, I haven't fully appreciated the wonder of Simpson's paradox until I run through real problems in practice. Simpson's paradox is mentioned at the beginning of most introductory statistics books. Basically, it says (according to wiki) a trend that appears in several different groups of data might disappear or even reverse when these groups are combined.
  • If all the cities in a country have higher GDP per capita after 10 years, does it mean that the country as a whole has higher GDP per capita?
  • If a treatment is better (higher success rate) for both group A patients and group B patients, does it mean this treatment is better for group A and B combined?
  • If the profit-to-income ratio is higher for every product for company A compared to company B, does it mean company A has higher profit-to-income? 

The answer is "not necessarily". And for the same reason, it is meaningless to take an unweighted average for a ratio measurement.

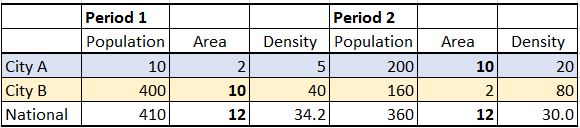
Let me give an example using density. Density is the ratio of the population divided by city area. Let's assume a country with 2 cities: A and B. From period 1 to 2, both cities have more than doubled their density (4 times and 2 times). If we take the direct average of the density of city A and city B, we would wrongly argue that the average density of the nation has more than doubled, while the real density of the nation has decreased by 12%

I made up these numbers, the trick is simply to give the period 1 denser city (B) more weights (Area), and give the period 2 less dense city (A) more weights. I have held the total area to be the same, otherwise, the result could be more dramatic. 

A minor issue is that if the areas can be held constant. Then if every city is denser the country will be denser for sure. It would be impossible to reverse the trend, but the error could still be tremendous. In the example below, real density has only increased by 30%, but an unweighted average of period 2 leads to a density 3 times higher than period 1 (130 compared to 35).


For real urban data, like in Colombia, since all the cities have growing urban extents, an unweighted average would be less biased, but still wrong. 

Comments

Post a Comment

Popular posts from this blog

Power-law distribution (Pareto)& Zipf's Law: connection and how to fit the distribution of global city population

-
Image
- This post counts for 3 days. - In short,  We use the histogram to outline the distribution, use rank-frequency plot (log-log plot) to identify the power-law distribution, and use maximum likelihood estimation to obtain the parameters. -  I will show 1 st , how the power-law function CDF and PDF can be derived from Zipf CDF; and 2 nd , this least square estimation by excel is wrong and how to get the right one. Historical background on the power-law distribution. - Power-law distribution is as common as normal distribution in the real world. In the 19 th century, Italian economist Pareto realized that 20% of the population owns 80% the wealth, which is the famous 80/20 rule. He later named the power-law distribution as Pareto distribution, which is what we studied in the probability course. - In the 20 th century, another main contributor, Zipf made a similar discovery in linguistics about the frequency of words used. - Besides social wealth, many things follow a hig
Read more

How to Draw Heatmap with Colorful Dendrogram

-
Image
Heatmap with Dendrogram: Color Branches and Labels This data visualization example include: * Hierarchical clustering, dendrogram, and heat map based on normalized odds ratios * The dendrogram was built separately to give color to dendrogram’s branches/labels based on clusters using  dendextend * Heatmap is made by  heatmap.2  from  gplots  using the built dendrogram * The rows are sorted by means from highest to lowest, it can be done in either the dendrogram or the  heatmap.2 * Use color palettes from  colorspace Data YRBSS (Youth Risk Behavior Surveillance System) survey data from CDC. This example plots the odds ratios of 63 behavioral questions on one question regarding disordered eating. The odds ratios are median centered by column and log2 transformed Version 1: Color both the branches and labels library (curl) # read file from google drive library (gplots) # heatmap.2 library (dendextend) # make and color dendrogram library (colorspace) #
Read more

The Weighted Standard Deviation

-
Image
I have revised the figures in the Conflicts in Colombia paper to add weighted s.e. Together with confidence intervals. Turns out to be not that complicated. Weighted s.d.: Add { geom_errorbar(aes(ymin=..., ymax=...), width = 0.2 } in ggplot2 to add the confidence interval into plots: The paper discussed how conflicts in Colombia makes cities develop more sluggish and denser. I will work more on it in the later posts. The complete R code for the figure # weighted means for global 200 sample ggplot(data=m4_mean_g_g200, aes(x=year, y=wm, group=Group, color=Group, shape=Group))+ geom_point(size= 4 )+ geom_line(size= 1 )+ geom_errorbar(aes(ymin=CI_low, ymax=CI_high), width= .2 )+ ggtitle( "Urban Density Change Over Time in 200 Cities" ) + labs(x= "Year" , y= "Average City Density" , color = "" , shape= "" ) + scale_y_continuous(limits = c( 30 , 150 ))
Read more