The two most well-established regularity about city size
Yesterday I basically said a distribution that can satisfy Zipf's law is a Pareto distribution. I need to clarify that Zipf's law is not the same as power-law. Zipf's law simply relies on the fact that the slope in log-log rank-to-size is approximately 1. So the population size of a city is inversely proportional to the rank of the size of the city. For example, in the US, the tenth-ranked city, Detroit, should have a size of 1/10 of New York.
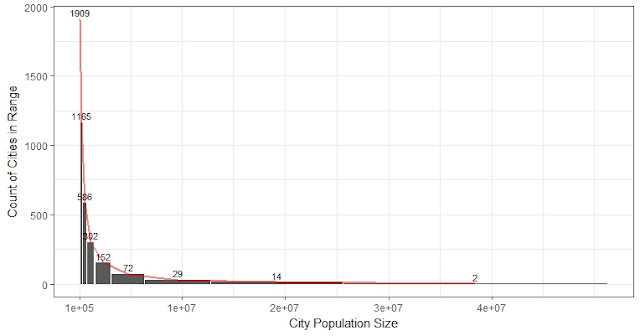
Today I was reading a good paper by Jan Eeckhout (2004): "Gibrat's law for all cities". He fit the distribution on the US 2010 census data on 25,359 cities, towns and villages ranging from 1 to over 8 million in population, and show power-law only fit for cities larger than a certain lower boundary. The lognormal distribution would fit the entire population (fit means KS test doesn't reject with 5% significance level). The two fitted distribution are more similar when the size is over Exp(12), which is 160 thousand, a little bit above the truncated size of the universe! Actually, for the universe, none of the distributions can be fit. Power-law cannot fit due to the extraordinary super cities on the right side of the distribution; lognormal cannot fit because the data is truncated at 100K.
The second regularity is that the city growth is a proportionate growth process (Gibrat’s Law) (Eeckhout 2004), which says growth rate doesn't depend on size. Large cities on average do not grower faster or slower than small cities. I did not realize this is already a widely established observation. And I found some interesting discussions on the reasons behind. The term proportionate growth was coined by biologist to describe the feature of growth in animals that different parts of the body grow at approximately the same rate (Dhar 2013). "In the case of humans, the body weight
increases by a factor of 30 or so. In the case of elephants, this factor is about 100. As the baby grows, different parts of the body grow at roughly the same rate." It is interesting to notice that this process cannot be totally controlled by DNA, hormone, or signaling molecules but rather seem to be the result of self-organization on a more basic level. I would guess just as organs are composed of individual cells, cities are composed of individuals and share such characteristic of being "self-organized". The model discussed in that paper is Abelian sandpile model, which is a cellular automaton that describes how patterns are generated from random processes.
From wiki: Conus textile exhibits a cellular automaton pattern on its shell.
More about cellular automation: https://en.wikipedia.org/wiki/Cellular_automaton

Today I was reading a good paper by Jan Eeckhout (2004): "Gibrat's law for all cities". He fit the distribution on the US 2010 census data on 25,359 cities, towns and villages ranging from 1 to over 8 million in population, and show power-law only fit for cities larger than a certain lower boundary. The lognormal distribution would fit the entire population (fit means KS test doesn't reject with 5% significance level). The two fitted distribution are more similar when the size is over Exp(12), which is 160 thousand, a little bit above the truncated size of the universe! Actually, for the universe, none of the distributions can be fit. Power-law cannot fit due to the extraordinary super cities on the right side of the distribution; lognormal cannot fit because the data is truncated at 100K.
The second regularity is that the city growth is a proportionate growth process (Gibrat’s Law) (Eeckhout 2004), which says growth rate doesn't depend on size. Large cities on average do not grower faster or slower than small cities. I did not realize this is already a widely established observation. And I found some interesting discussions on the reasons behind. The term proportionate growth was coined by biologist to describe the feature of growth in animals that different parts of the body grow at approximately the same rate (Dhar 2013). "In the case of humans, the body weight
increases by a factor of 30 or so. In the case of elephants, this factor is about 100. As the baby grows, different parts of the body grow at roughly the same rate." It is interesting to notice that this process cannot be totally controlled by DNA, hormone, or signaling molecules but rather seem to be the result of self-organization on a more basic level. I would guess just as organs are composed of individual cells, cities are composed of individuals and share such characteristic of being "self-organized". The model discussed in that paper is Abelian sandpile model, which is a cellular automaton that describes how patterns are generated from random processes.
From wiki: Conus textile exhibits a cellular automaton pattern on its shell.
More about cellular automation: https://en.wikipedia.org/wiki/Cellular_automaton




Comments