Fix a minor issue calculating geological distance when acos produces NaN

-

As well as how the distances between geological points were calculated

Calculating the distance between two points on the earth is fundamental to calculate all the measurements mentioned in earlier posts.
The distance in kilometers is calculated using the Spherical Law of Cosines:
d = acos( sin(lat1)*sin(lat2) + cos(lat1)*cos(lat2)*cos(long2-long1) )  * 6371 (km)
Step-by-step explanation:
The sin and cos functions take latitudes and longitudes input in radians in most softwares. For example, Shanghai has a coordination of (31.222, 121.458), its (lat1, long1) in radians is (31.222/180 * pi, 121.458/180 * pi) = (0.55, 2.12), pi = 3.14159...
The coordination for New York is (40.717, -74.004), in radian: (0.71, -1.29).

sin(lat1)*sin(lat2) + cos(lat1)*cos(lat2)*cos(long2-long1) 
= sin(0.55)*sin(0.71) + cos(0.55)*cos(0.71)*cos(-1.29 - 2.12)
= -0.28  ---> this output is a value from -1 to 1

 The angle AOB formed by A (Shanghai), O (Center of Earth), and B (New York) in the figure below (borrowed from: link, just to give an idea) is acos(-0.28) = 1.86 radians, or in degrees: 1.86/3.14*180 = 106.6°.
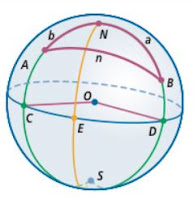
We use the angle in radians directly to get the length of the arc: 
d = acos(-0.283) * (radius of Earth) = 1.86 * 6371 = 11836 km. 
We can program this in R, or use package. Without rounding error in the calculation above, the more accurate result from R is 11859 km. In SAS there is a geodist function to get the same result. If we google the distance between Shanghai and New York the result is 11851 km. 

 The minor issue is: sometimes in R the acos function can return NaN while the input is shown as 1. Somehow the calculated input from (sin(lat1)*sin(lat2) + cos(lat1)*cos(lat2)*cos(long2-long1)) shown as 1 is not really 1 due to rounding of small decimals. If c = sin(lat1)*sin(lat2) + cos(lat1)*cos(lat2)*cos(long2-long1), using acos(pmin(c, 1)) to set the up bound to 1 avoids producing NaN. I use "pmin" (parallel min) here because c is a vector in my case. This issue was discussed in this post.

Comments

Post a Comment

Popular posts from this blog

Power-law distribution (Pareto)& Zipf's Law: connection and how to fit the distribution of global city population

-
Image
- This post counts for 3 days. - In short,  We use the histogram to outline the distribution, use rank-frequency plot (log-log plot) to identify the power-law distribution, and use maximum likelihood estimation to obtain the parameters. -  I will show 1 st , how the power-law function CDF and PDF can be derived from Zipf CDF; and 2 nd , this least square estimation by excel is wrong and how to get the right one. Historical background on the power-law distribution. - Power-law distribution is as common as normal distribution in the real world. In the 19 th century, Italian economist Pareto realized that 20% of the population owns 80% the wealth, which is the famous 80/20 rule. He later named the power-law distribution as Pareto distribution, which is what we studied in the probability course. - In the 20 th century, another main contributor, Zipf made a similar discovery in linguistics about the frequency of words used. - Besides social wealth, many things follow a hig
Read more

How to Draw Heatmap with Colorful Dendrogram

-
Image
Heatmap with Dendrogram: Color Branches and Labels This data visualization example include: * Hierarchical clustering, dendrogram, and heat map based on normalized odds ratios * The dendrogram was built separately to give color to dendrogram’s branches/labels based on clusters using  dendextend * Heatmap is made by  heatmap.2  from  gplots  using the built dendrogram * The rows are sorted by means from highest to lowest, it can be done in either the dendrogram or the  heatmap.2 * Use color palettes from  colorspace Data YRBSS (Youth Risk Behavior Surveillance System) survey data from CDC. This example plots the odds ratios of 63 behavioral questions on one question regarding disordered eating. The odds ratios are median centered by column and log2 transformed Version 1: Color both the branches and labels library (curl) # read file from google drive library (gplots) # heatmap.2 library (dendextend) # make and color dendrogram library (colorspace) #
Read more

The Weighted Standard Deviation

-
Image
I have revised the figures in the Conflicts in Colombia paper to add weighted s.e. Together with confidence intervals. Turns out to be not that complicated. Weighted s.d.: Add { geom_errorbar(aes(ymin=..., ymax=...), width = 0.2 } in ggplot2 to add the confidence interval into plots: The paper discussed how conflicts in Colombia makes cities develop more sluggish and denser. I will work more on it in the later posts. The complete R code for the figure # weighted means for global 200 sample ggplot(data=m4_mean_g_g200, aes(x=year, y=wm, group=Group, color=Group, shape=Group))+ geom_point(size= 4 )+ geom_line(size= 1 )+ geom_errorbar(aes(ymin=CI_low, ymax=CI_high), width= .2 )+ ggtitle( "Urban Density Change Over Time in 200 Cities" ) + labs(x= "Year" , y= "Average City Density" , color = "" , shape= "" ) + scale_y_continuous(limits = c( 30 , 150 ))
Read more