Interesting findings on weights

-

  • Assume I have several variables to study from the sample, should we apply same or different weight?
  • When will the weights be helpful to make the sample mean closer to the population mean?
  • Are some weights more helpful than others depending on the nature of the variable?
Our case is especially confusing, because different from a common study, the subject is not an individual, but a city! Most variables are city-based: city area, block size, etc. But each city has its own population size, and some variables are individual-based: like GDP per capita. GDP per capita is measured by the city, but its nature is an individual-level variable. We should treat them differently. 

Our data have offered a great opportunity to test these questions. We have a sample of 200 cities for which we have measured more than a hundred variables. These 200 samples were drawn from the 4231 global cities (named as the universe of cities), which is the real population of the sample. We happen to have several variables for the universe: city population size, population growth rate, city GDP, city GDP per capita and the airport score mentioned in the earlier posts.

We divided the universe by 8 region, 4 population size categories and 3 country size categories (number of cities in the country) into 8*4*3 = 96 strata. Then the 200 samples were sampled unevenly from these strata. For each stratum i, if there are N(i) universe cities in it, among which we have sample n(i) cities.

1. Then we have the first kind of weight: the most common kind of weight used to balance sampling bias: 
> City Weight: w(i) = N(i) / n(i), this weight is same for sampled cities in each stratum.

 2. The second way: for each stratum i, if the total city population in it is P(i), and the total city population for the several sampled cities from this stratum is p(i):
> Population Weight: w(i) = P(i) / p(i) 

3. The third potential way was perhaps designed for individual-level data (e.g. personal income). It adjusts for both sampling bias and population: I call it 'Individual Weight'. And it has a different weight for each city, while all the other ways have the same weight for cities from the same stratum. 
> Individual Weight: w(city_j) = N(i) / n(i) * population(city_j)

(The 1st and 3rd types are the weights we originally used to check growth rate is the earlier paper.)

4. The last kind is a post-stratification weight created from re-dividing the population into clusters using key universe variables we have. I "invented" it and I have not read similar approach elsewhere. In short, we extract factors through factor analysis using all the universe variables, standardize, then apply a clustering analysis to group them into clusters. Assume there are 30 clusters, and cluster (i) has Nc(i) universe cities, from which nc(i) belong to the sample:
> Clustering Weight: w(i) = Nc(i) / nc(i)

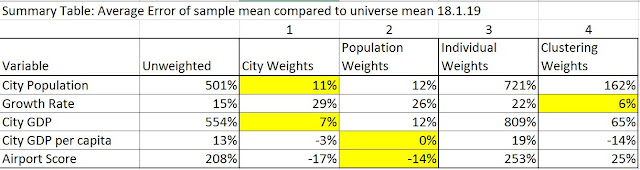
I have tested the difference of sample means against the "true population means" using each weight for 5 variables. The conclusions in short are:
  • The effect of the weight depends on the nature of each variable, and if this variable correlates with what is used to create the strata (in our case: region, population, #city in a country).
  • The city weight performs similarly well to population weight.
  • Population weight, which is P(i)/p(i), and is same for cities in the same stratum, is the best for individual-based variable: GDP per capita
  • Individual weight is not useful, sometimes it backfires by overstating the influence of population.
  • Clustering weight only works best for growth rate, because growth rate was used to build the clusters. 


 Further comments
If the weight does not correlate with the variable, applying it won't make any difference. Population growth rate almost does not correlate with anything else, thus better leave it unweighted. The original 96 strata were built on 8 regions in the world and 4 population groups. What distinguishes the 8 regions in the world (East Asia, Africa, Europe, etc) beside their locations? Their GDP per capita. No wonder population, GDP, GDP per capita, and Airport Score which correlates strongly with all these variables (especially with GDP) all can be rescued by applying weight. I have performed hypothesis testing for all of them, the details are complicated but in short, those highlighted above, along with everything weighted by city weight and population weight are not statistically different from the true values. So city weight and population weight work for all of them, even growth rate.

This post is too long. But it is a complicated issue to explain. There are more related topics, e.g. be especially careful with a ratio variable.

Comments

Post a Comment

Popular posts from this blog

How to Draw Heatmap with Colorful Dendrogram

-
Image
Heatmap with Dendrogram: Color Branches and Labels This data visualization example include: * Hierarchical clustering, dendrogram, and heat map based on normalized odds ratios * The dendrogram was built separately to give color to dendrogram’s branches/labels based on clusters using  dendextend * Heatmap is made by  heatmap.2  from  gplots  using the built dendrogram * The rows are sorted by means from highest to lowest, it can be done in either the dendrogram or the  heatmap.2 * Use color palettes from  colorspace Data YRBSS (Youth Risk Behavior Surveillance System) survey data from CDC. This example plots the odds ratios of 63 behavioral questions on one question regarding disordered eating. The odds ratios are median centered by column and log2 transformed Version 1: Color both the branches and labels library (curl) # read file from google drive library (gplots) # heatmap.2 library (dendextend) # make and color ...
Read more

Power-law distribution (Pareto)& Zipf's Law: connection and how to fit the distribution of global city population

-
Image
- This post counts for 3 days. - In short,  We use the histogram to outline the distribution, use rank-frequency plot (log-log plot) to identify the power-law distribution, and use maximum likelihood estimation to obtain the parameters. -  I will show 1 st , how the power-law function CDF and PDF can be derived from Zipf CDF; and 2 nd , this least square estimation by excel is wrong and how to get the right one. Historical background on the power-law distribution. - Power-law distribution is as common as normal distribution in the real world. In the 19 th century, Italian economist Pareto realized that 20% of the population owns 80% the wealth, which is the famous 80/20 rule. He later named the power-law distribution as Pareto distribution, which is what we studied in the probability course. - In the 20 th century, another main contributor, Zipf made a similar discovery in linguistics about the frequency of words used. - Besides social wealth, many things fol...
Read more

eXtreme Gradient Boosting (XGBoost): Better than random forest or gradient boosting

-
Image
Ensemble Methods 1. Random Forest 2. Gradient boosting 3. Extreme Gradient Boosting Compared to Lasso and Best-subset Lasso Best-subset Compare MSEs Code I recently had the great pleasure to meet with Professor Allan Just and he introduced me to eXtreme Gradient Boosting (XGBoost). XGBoost is “one of the most loved machine learning algorithms at Kaggle”, it somehow combines the advantages of random forest and boosting. We will see later its predictive ability is indeed very strong. In the earlier post  Model Selection using Lasso and Best Subset  I mainly focused on model selection by best-subset, stepwise, or lasso. This post will focus on ensemble method: random forest, Gradient boosting, and eXtreme Gradient Boosting (XGBoost). An ensemble method is a technique that combines the predictions from multiple machine learning algorithms together to make more accurate predictions than any individual model. 1. Random Forest Use library  ran...
Read more