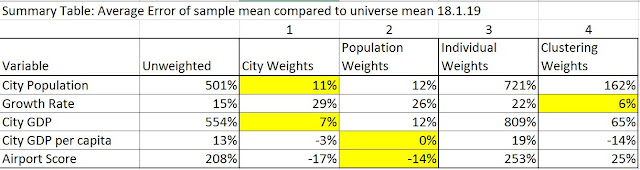
The two most well-established regularity about city size

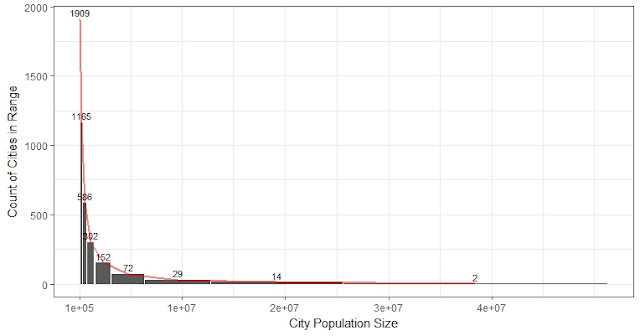
Yesterday I basically said a distribution that can satisfy Zipf's law is a Pareto distribution. I need to clarify that Zipf's law is not the same as power-law. Zipf's law simply relies on the fact that the slope in log-log rank-to-size is approximately 1. So the population size of a city is inversely proportional to the rank of the size of the city. For example, in the US, the tenth-ranked city, Detroit, should have a size of 1/10 of New York. Today I was reading a good paper by Jan Eeckhout (2004): "Gibrat's law for all cities". He fit the distribution on the US 2010 census data on 25,359 cities, towns and villages ranging from 1 to over 8 million in population, and show power-law only fit for cities larger than a certain lower boundary. The lognormal distribution would fit the entire population (fit means KS test doesn't reject with 5% significance level). The two fitted distribution are more similar when the size is over Exp(12), which is 160 thousand...