More on the Zipf's Law and Gibrat's Law
Since last Wednesday I have been updating the paper on the universe of cities. I have further simplified the statistical contents as statistics is usually confusing. It is a good learning for me, to focus on the findings, and make statistics simpler. Knowing that less is more, the restraint from lecturing statistics is something to be learned.
It also occurred to me when rewriting the paper that the real findings are not that our data comply with the rank-size rule and proportionate growth mentioned in the last post, but rather, the data don't fit perfectly with these two regularities.
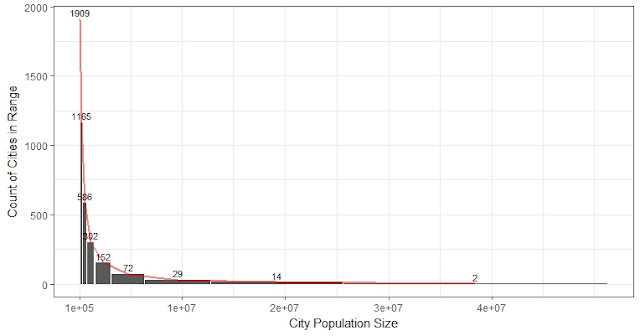
The well-established rank-size rule describing city population size has its limit. It cannot fit the whole distribution if truncated at the lower end, as shown by Jan Eeckhout (2004). It cannot fit very large cities if pool the universe of cities together instead of looking into each country separately, as shown by our study. The power-law function is a mathematically simple and elegant model but has its limitations. The second regularity of proportionate growth also depends on the subject under study. During the past several decades, it applies to the developed counties but not the whole universe.
In this figure, I plot the fitted power-law function in Zipf CDF format: log (city population size) vs. log(rank of the city). There are data from three time periods: 1990, 2000 and 2010.
We can see obviously from the figure that the power-law function underlying the rank-size rule does not fit very well when the city population size is very large, especially above the dotted line (1E6.5) in Figure 8. Although it is worth noticing that power-law distribution fits most of the cities, since only 117 cities (2.8%) in the 2010 universe have population sizes larger than 1E6.5, the function cannot fit the complete universe of cities.
Actually, it turns out the exponents also vary a lot in countries. And power-law exponents are very sensitive to the definition of city and sample size, as observed by Rosen and Resnick in an early paper in 1980. It would be very helpful to do literature review earlier.
I also just realized these two laws are the two sides of the same coin. Gabaix (1999) shows that if cities grow randomly according to Gibrat’s Law, the limit distribution of city size converges to obey Zipf’ Law.
It also occurred to me when rewriting the paper that the real findings are not that our data comply with the rank-size rule and proportionate growth mentioned in the last post, but rather, the data don't fit perfectly with these two regularities.
The well-established rank-size rule describing city population size has its limit. It cannot fit the whole distribution if truncated at the lower end, as shown by Jan Eeckhout (2004). It cannot fit very large cities if pool the universe of cities together instead of looking into each country separately, as shown by our study. The power-law function is a mathematically simple and elegant model but has its limitations. The second regularity of proportionate growth also depends on the subject under study. During the past several decades, it applies to the developed counties but not the whole universe.
In this figure, I plot the fitted power-law function in Zipf CDF format: log (city population size) vs. log(rank of the city). There are data from three time periods: 1990, 2000 and 2010.
(The figure is weird to people studying statistics as the x-axis and y-axis are the opposite to a histogram, but this is how the size-rank rule is illustrated conventionally.)
We can see obviously from the figure that the power-law function underlying the rank-size rule does not fit very well when the city population size is very large, especially above the dotted line (1E6.5) in Figure 8. Although it is worth noticing that power-law distribution fits most of the cities, since only 117 cities (2.8%) in the 2010 universe have population sizes larger than 1E6.5, the function cannot fit the complete universe of cities.
Actually, it turns out the exponents also vary a lot in countries. And power-law exponents are very sensitive to the definition of city and sample size, as observed by Rosen and Resnick in an early paper in 1980. It would be very helpful to do literature review earlier.
I also just realized these two laws are the two sides of the same coin. Gabaix (1999) shows that if cities grow randomly according to Gibrat’s Law, the limit distribution of city size converges to obey Zipf’ Law.



Comments