Logistic regression using YRBSS data: the 2nd example discussing being sad or depressed

(Compared to the last post on risk to attempt suicide, the main difference is that the interaction effect is not significant.)

The hypothesis is: Are the sexual minority (LGBT) kids who use the computer more often (meaning > 5 hours), more likely to be sad or depressed? 

Again, this question is an incomplete one.

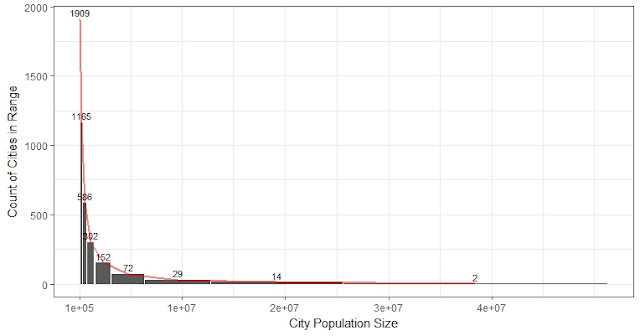
The big picture in front: why >5 hours is a reasonable break. 

For all the kids, do kids who use PC more than __ hours more likely to be depressed than kids who use PC less than such hours? 

2 hours or 3 hours are not significant. 4 hours is weakly significant, 5 hours is significant. OR = 1.63 (1.44 – 1.84). 41% of all the kids use PC more than 5 hours, which is a large enough amount. I see no reason to go into the more detailed breakdowns within 5 hours.

8% of all the kids belong to the LBGT group. Since there are 13,862 kids in total, 8% represents about 1,145 kids. 

In the LGBT group, 52% use PC more often, while in the majority group, 40% use PC more often. So LGBT group is indeed more likely to use PC more often (without talking about other risks): OR = 1.62 (1.43 - 1.84).

All the numbers reported are weighed by survey weight. 

There are 3 ways to complete the question:

1.     Is the LGBT group who use the computer more often, more likely to be sad or depressed than the majority group who also use the computer more often? 

2.     Is the LGBT group who use the computer more often, more likely to be sad or depressed than the LGBT group who use the computer less often? 

3.    Assume that the LGBT group is more likely to be said or depressed than the majority group no matter they use PC more often or less often, then which group is even riskier for the LGBT group compared to the majority, the use-PC-more-often group, or use-PC-less-often group?

The three coefficients estimated from the logistic regression will answer all the three questions. But let's looks at them separately by 2-by-2 contingency tables first:

1. For the kids who use computers more often, is the LGBT group more likely to be sad or depressed than the majority group?

This is a 2-by-2 table between (QN68_New：LGBT/Majority Group) and (QN26_NEW：Be sad or depressed Y/N). For the kids who use PC more often: In the 597 LGBT kids, 65% are sad or depressed, while in the 5,072 majority kids, only 31% are sad or depressed. Among the kids who use computers more often, LGBT group is more likely to be sad or depressed than the majority group. The OR = 4.038 (3.38 - 4.83)  (a). 

Then how about the kids who use PC less often? For the kids who use computers less often, the LGBT group is also more likely to be sad or depressed than the majority group.

For the kids who use computers less often: 55% of the 532 LGBT kids are sad or depressed and 23% of the 6,736 majority kids are sad or depressed. The OR = 4.16 (3.47 - 4.97)  (b)

So the answer to question 1 is: (No matter use PC more or less often, LGBT group is more likely to be sad or depressed than the majority group.)

But since the OR (a) = 4.038 and OR (b) = 4.16 are very close. We cannot tell the answer to question 3 yet. In both LGBT and majority groups, using PC more often is associated with higher risk to be sad or depressed. But we cannot tell which group is under a stronger influence by using PC. 

In the case of attempting suicide, the OR has almost doubled for the LGBT kids who use PC less often, so the answer is easy that in the use-PC-less-often group, LGBT kids are even more likely than the majority to attempt suicide (see that post for details). 

2. For the LGBT group, are LGBT kids who use the computer more often, more likely to be sad or depressed than LGBT kids who use the computer less often?

Among the 532 LGBT kids who use PC less often, 55% are sad or depressed; among the 597 LGBT kids who use PC more often, 65% are sad or depressed. Using PC more often is associated with being sad or depressed with an OR = 1.525  (c)  (1.2 - 1.94) within the LGBT kids. 

So the answer to question 2 is: (Yes, the LGBT kids who use the computer more often are more likely to be sad or depressed than LGBT kids who use computers less often.)

But could this be the same for the kids in the majority group? 

Among the 7,540 majority kids who use PC less often, 23% are sad or depressed. Among the 5,072 majority kids who use PC more often, 32% are sad or depressed. The majority kids who use computers more often are more likely to be sad or depressed than the majority kids who use computers less often with an OR = 1.570 (d) (1.2 - 1.94).

Again, since OR (d) and (c) are pretty close, it seems the effect of using more PC on being sad or depressed is similar to a kid no matter he is LGBT or not, which is also a finding in itself. As we can show in the logistic regression below, the interaction term is not statistically significant, confirming this finding that odds ratio (a) and (b), as well as (c) and (d) are not significantly different.

******

The logistic regression model (use proc surveylogistic in SAS) to address these questions is: 

Formula:

logit(P(Be sad or depressed)) = beta0 + beta1 (LGBT) + beta2 (Use PC more often) 
+ beta3 (LGBT Group) (PC Use for Long Hours )
Fitted:

logit(P(Be sad or depressed)) = -1.219 + 1.425 (LGBT) + 0.451 (Use PC more often) 
- 0.029  (LGBT Group) (PC Use for Long Hours )

LGBT: 0/1, with baseline 0: majority group;
Use PC more often: 0/1, with baseline 0: use PC less often;

(1).     beta0: log odds ratio (OR) for the majority group who use PC less often; 

(2).     beta0 + beta1: log OR for the LGBT group who use PC less often;

(3).     beta0 + beta2: log OR for the majority group who use PC more often;

(4).     beta0 + beta1 + beta2 + beta3: log OR for the LGBT group who use PC more often

*log odds ratio is the log(odds ratio), so exp(beta) = odds ratio.

(2) - (1) = beta1: the log OR (the risk towards being sad or depressed) for LGBT vs. majority group for those who use PC less often.

exp(beta1) = 
exp(1.425) = 4.16, 

we have obtained the same OR (b) by contingency table in question 1.

(3) - (1) = beta2: the log OR for use PC more often vs. less often for majority group

exp(0.451) = 1.57, same as the OR (d) obtained in question 2. 

(4) - (2) = beta2 + beta 3: the log OR for use PC more often vs. less often among LGBT

exp(0.451 - 0.029) = 1.525, which is the same as (c) in question 2. 

(4) - (3) = beta1 + beta 3: the log OR for LGBT vs. majority among those who use PC more often

exp(1.425 - 0.029) = 4.039, which is the same as (a) in question 1. 

So the question is, is 1.525 significantly different from 1.57, and 4.039 different from 4.16? 

Since the interaction term is not statistically significant, we say they are not significantly different. To sum up, kids who use PC more often are more likely to be sad or depressed than those who use PC less often, no matter he is LGBT or the majority. Kids who are LGBT are more likely to be sad or depressed than the majority, no matter how long he uses the computer. 

The corresponding SAS program and output:

proc surveylogistic data = new;

class PCAbove5  QN68_New QN26_NEW (ref='Not Sad')  / param = ref;

model   QN26_NEW =   QN68_New  | PCAbove5;

weight weight;

strata stratum;

run;