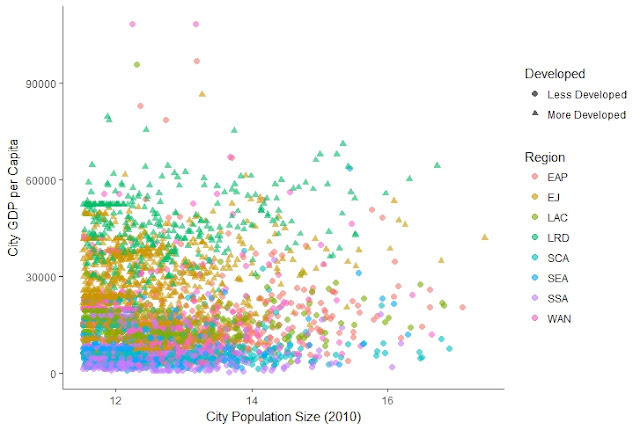
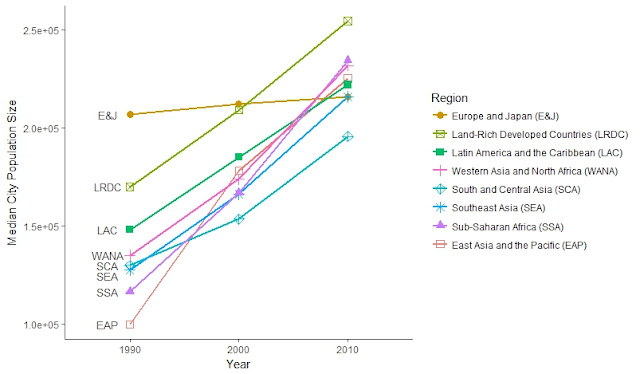
Survey data analysis using SAS
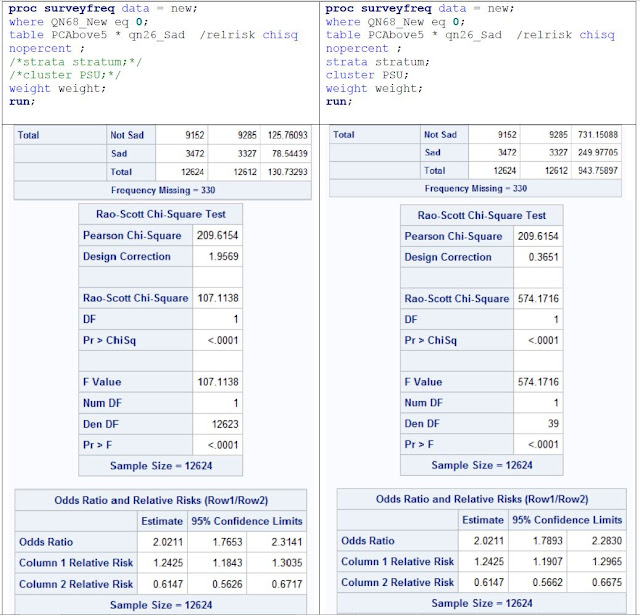
Notes on analyzing survey data using SAS Work a lot on the survey data this week. It turns out that when using statistical package for survey data, it is critical to include all the three variables: clusters (PSU), strata, and weights. But the difference is smaller if without the cluster and strata information. *** *** For example, These two procedures in SAS (both w/o weights) will produce the same contingency table (frequency count) and thus same odds ratio (since it is calculated from frequency). The confidence intervals around OR are slightly different. proc freq data = new; table PCAbove5 * qn26_Sad /relrisk chisq nopercent ; run; proc surveyfreq data = new; table PCAbove5 * qn26_Sad /relrisk chisq nopercent ; strata stratum; cluster PSU; run; If weights are added to both procedures, we can get the same weighted frequency and OR. The OR is different from the unweighted OR. The confidence interval around OR gets wider. *** *** The differ...